2025年共通テスト 数学ⅠA対策|時間配分・出題傾向・時短テクニックを徹底解説
2024.11.19 大学受験オススメ情報 富士校
荷川取

目次
2025年共通テスト 数学ⅠA対策|時間配分・出題傾向・時短テクニックを徹底解説
2026年度の最新傾向はこちら
共通テスト数学は、従来のセンター試験とは異なる形で進化し続けており、2023年度の試験では試験時間や問題の構成に大幅な変更が加わりました。この新たな形式に対応するには、基礎的な学力に加えて、文章の読解力や柔軟な思考力が不可欠です。本記事では、2025年度の変更点から具体的な対策法・テクニック・出題傾向までを詳しく解説し、受験生が共通テスト数学で高得点を取るための道筋を徹底解説します!
2025年度共通テスト数学の大きな変更点:試験時間と問題量の増加
「数学Ⅰ・A」では、大問5問から、大問4問(新課程)に変更となりました。
選択問題であった数Aの「整数」なくなり、「図形の性質」と「場合の数・確率」が必答問題に変更となります。
それ以外はほとんど変化がなく、配点や難易度は従来通りです。
(補足)
2023年度から試験時間が60分から70分に延長されました。この変更に伴い、ページ数は従来の約1.5倍に増え、問題文の文字数も2020年度の約4,000字から約6,000字へと大幅に増加しています。長い文章を正確に読み取り、短時間で計算を終えるスキルがこれまで以上に求められるようになりました。
センター試験から共通テストへの移行:出題の本質的な変化
基本的なスキルから「思考力・判断力・表現力」重視へ
センター試験では公式や定理を直接使う問題が中心でしたが、共通テストでは**「日常生活の状況を数理的に分析する問題」や「2人の生徒の会話を基に解法を探る問題」**など、現実の問題を数学でモデル化する力が問われるようになっています。
これらの問題は公式の暗記や基本的な計算能力だけでは対応できず、文章の中から必要な情報を読み取る力や、それを活用して解決する柔軟性が必要です。
問題構成の具体例
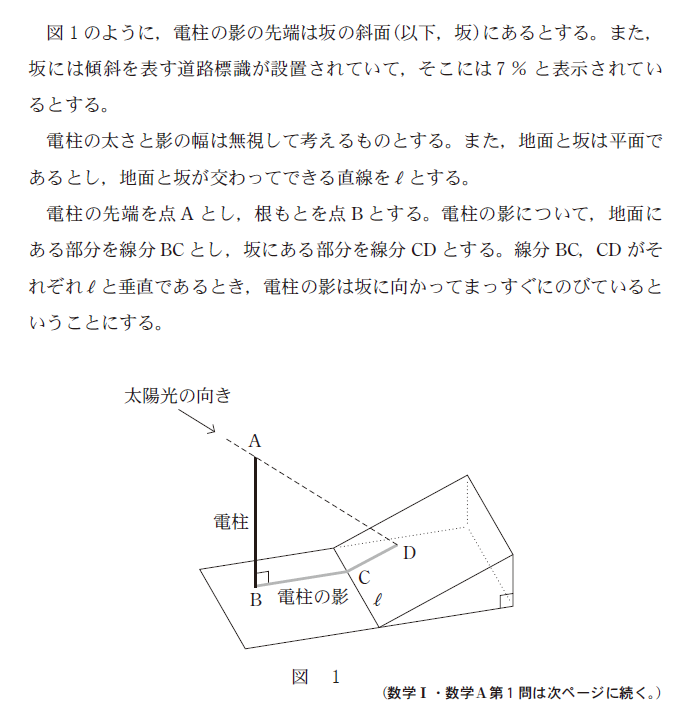
①日常生活の状況を数理的に分析する問題
買い物や気象観測などを題材に、数値化や関係性を解析する問題。
②2人の生徒の会話を基に解法を探る問題
登場人物の発言を基に、最適な解法を考える問題。

共通テスト2024年本試験から引用
おすすめ時間配分例
数学ⅠAの配点と時間配分例
| 大問 | 分野 | 配点 | 時間配分 |
|---|---|---|---|
| 1 | [1]数と式 | 30 | 8分 |
| [2]図形と計量 | 12分 | ||
| 2 | [1]2次関数 | 30 | 12分 |
| [2]データの分析 | 8分 | ||
| 3 | 場合の数と確率 | 20 | 12分 |
| 4 | 図形の性質 | 20 | 12分 |
| 見直し | 6分 | ||
マークミスの対策・後回しにした問題を解きなおすため、見直し時間(6分)は必ず確保しておきましょう。
大問別出題傾向&時短テクニック
大問1 数と式/図形と計量(20分):[1]数と式で時間を稼ぐ
【頻出問題】
[1]数と式:有理数・無理数/絶対値/対称式
[2]図形と計量:測量、縮尺、正弦定理と余弦定理の利用
【時短・解答テクニック】
- 空間図形が来たら平面図を抜き出す:空間図形になると受験生の正答率が一気に悪くなりますが、原理はあくまで平面です。見たい三角形・四角形だけを書き直しましょう。
- 選択肢を見ながら解く:選択肢に目を通してから本文を読むことで、効率的に答えを導けます。
- 直角三角形から優先的にみる:三角比が利用しやすい直角三角形を優先的に注目すると効率的です。
大問2 2次関数/データの分析(20分):情報の正確な読み取りがカギ
【頻出問題】
[1]2次関数:グラフのプロット/最大最小
[2]データの分析:箱ひげ図・ヒストグラム・散布図の読み取り/相関係数・共分散
【時短・解答テクニック】
- 「問題後半を見る」テクニック: 問題文が長くて複雑な場合、いきなり読むのではなく、後半の設問部分を先に確認してから問題に取り組むと、状況を把握しやすくなります。
- データの変化や比較に注目:年ごとの変化やデータの多寡など、質問で求められる情報に絞って見ると無駄がありません。
- 「具体的な値を使う」アプローチ :数字が抽象的で理解しにくい場合、具体的な数値を代入してイメージを掴む練習をすることで、解答に近づけます。
大問3 場合の数と確率(12分):比較的文章量も少ないため、得点源に
【頻出問題】
ゲームの確率/条件付確率
※期待値が新たに範囲に含まれるため、本年度共通テストでの出題が予想される。
【時短・解答テクニック】
- 条件付確率・期待値の計算に備える:先に後半で必要になる数値を確認し、わかりやすくメモを取っておくことで、後からスムーズに回答しやすくなります。
- 選択肢を入れて試す: 証明問題や論理問題では、選択肢を実際に当てはめてみることで正しい答えを導きやすくなります。
- 無駄な情報は読み飛ばす:設問で問われる部分以外の詳細にこだわらず、設問に関係のある要点だけを探しましょう。
大問4 図形の性質(12分):公式を使える図形の特徴・回答欄をインプットする
【頻出問題】
チェバ・メネラウスの定理/方べきの定理/外接円・内接円
【時短・解答テクニック】
- 線分の比を求める方法をインプット:線分の比を求める問題は共通テスト頻出。チェバ・メネラウス、方べきの定理、三角形の面積比、相似は最低限頭に入れておく。
- 問題ごとに簡単な図を描きなおす:与えられた図にはじめから最後までの情報を書き足していくと、使わない情報と使う情報が入り乱れて、着眼点がわかりづらい。簡単だが特徴をつかんだ図に、そこで必要な情報に絞って書き込む。
高得点を目指すための具体的な学習ステップ
①基礎固め
公式や定理をしっかり理解し、計算力を磨きましょう。市販の網羅型問題集(例:青チャート)を使い、基礎を徹底的に固めることが重要です。青チャートでは、レベル2とレベル3の問題を重点的に解くことで、効率良く基礎力を身につけられます。
②共通テスト形式に慣れる
過去問や予想問題を解いて、共通テスト特有の「会話形式問題」や「日常生活を題材にした問題」に対応できるようにしましょう。特に長文読解の要素を含む問題では、文章の中から数理的な関係性を読み取る訓練が必要です。
③時間配分を意識した演習
試験時間が限られているため、効率的な時間配分が重要です。
④問題演習で「考える力」を鍛える
問題を解く際に以下の点を意識して取り組むと、「思考力」「判断力」が身につきます。
- 「この問題はどう解くべきか?」
- 「なぜこの解法が適切なのか?」
- 「必要な情報はどこにあるのか?」
⑤見返せるノートを作る
解いた問題を振り返り、つまずいた箇所やその解法のポイントをノートに記録する習慣をつけましょう。ノートに「考え方」や「解き方のプロセス」を書き留めることで、反復学習が効果的になります。
⑥過去問と予想問題を活用
特に2023年度以降の形式に沿った予想問題を重点的に解き、時間内に解答する練習を行いましょう。マークミス防止のため、解答用紙を使用することもおすすめです。
投稿者
荷川取
富士校舎の校舎長荷川取です!
▲▲クリックして荷川取のブログ一覧(85ブログ公開中)を見る

