はじめに｜数学ⅡBCは新形式2年目、勝負の舞台へ！

2025年度から始まった「数学ⅡBC」。
数学Ⅱの必答3題と、数学B・Cの選択4題から3題を解き、合計6題を70分で仕上げるという、非常にハードな試験です。

新形式2年目となる2026年度は、形式が定着する一方で、難化の波が押し寄せる可能性が高いと予想されています。
つまり、ただ「慣れる」だけでは足りません。問題を読み解き、時間を操り、自分の得点力を最大化できるか――ここが真の勝負どころです。

この記事では、

・数学ⅡBCの基本情報

・時間配分のコツ

・実戦で効く時短テクニック

・2026年度の出題予想

を徹底的に紹介します。

「時間が足りない…」「どの選択問題を選べばいいか迷う…」
そんな不安を解消し、本番で数学ⅡBCを得点源に変える道筋を一緒に見つけていきましょう。

---

2. 共通テスト数学ⅡBCの基本情報｜出題形式と配点ルールを正しく理解しよう

数学ⅡBCは2025年度から形式が変更され、2026年度も同じ構成で実施される見込みです。
まずは「時間・配点・出題分野」を整理して把握しましょう。

基本情報

項目	内容
試験時間	70分
大問数	6題（必答3題＋選択3題）
満点	100点
解答形式	マークシート方式
特徴	文章量が多く、図表やグラフを伴う問題が多い

出題構成と配点（2025年度形式）

大問	分野	必答／選択	配点	特徴
第1問	三角関数	必答	15点	加法定理やグラフを中心に出題
第2問	指数・対数関数	必答	15点	指数方程式・対数方程式、グラフの性質など
第3問	微分・積分	必答	22点	最大・最小、面積計算、グラフの考察
第4問	数列	選択	16点	漸化式、和の計算、数学的帰納法など
第5問	ベクトル	選択	16点	内積・距離・面積、図形問題との融合
第6問	統計的推測	選択	16点	標本分布、仮説検定、母平均の区間推定など
第7問	複素数平面	選択	16点	複素数の表示、回転・図形的意味の活用

形式のポイント

・必答問題（Ⅱ分野）で52点が配分されており、ここを安定させることが合格ライン突破のカギ。

・選択問題（B・C分野）は4題中3題を選ぶ形式で、得意不得意が大きく点に影響する。

・新課程の分野（統計的推測・複素数平面・二次曲線）が含まれ、暗記だけでは太刀打ちできない“概念理解”が求められる。

---

おすすめ時間配分と戦略

数学ⅡBCは70分で6題を解かなければならない試験です。
1題あたりにかけられる時間は平均11〜12分。しかし実際には、大問ごとに処理量や計算の複雑さが異なるため、メリハリをつけた時間配分が必須です。

時間配分の目安

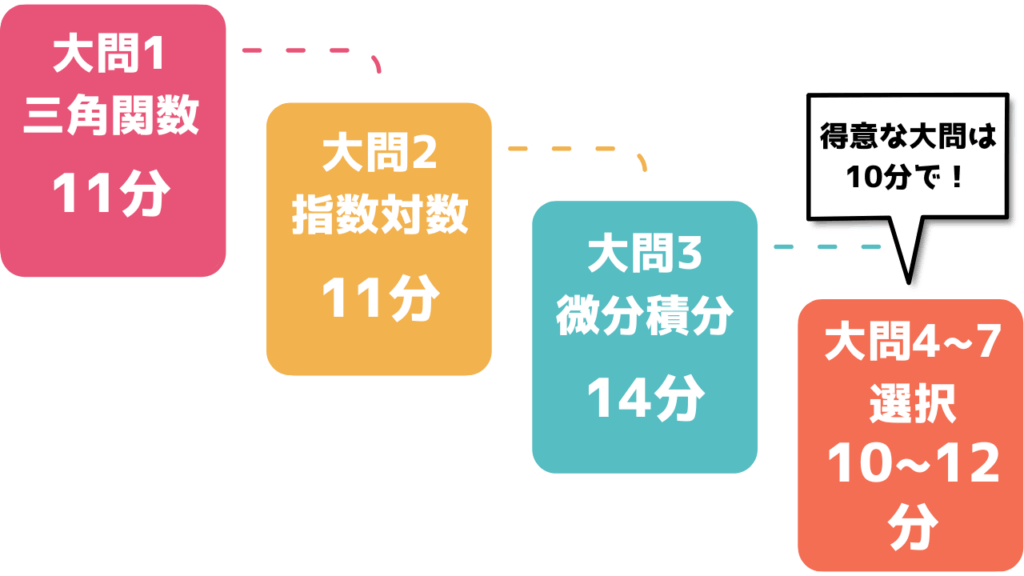
戦略の立て方

1.最初は必答問題でリズムを作る

　三角関数・指数対数は比較的解きやすい分野。ここで時間を守って解き切ると精神的に安定する。

2.微積分は外せない得点源

　計算量が多い分、配点も最大。苦手でも「導関数を求める」「極値を出す」といった部分点を必ず拾う意識を持つ。

3.選択問題は“模試での練習結果”から選ぶ

　普段の演習で「自分が一番安定して解ける大問」を把握しておき、本番ではその大問から確実に解く。本番でどの大問を解こうか迷っている時間はない。

4.11分を超えたら一旦飛ばす

　「あと少しで解けそう」にハマると、他の大問に手を付けられず大失点に。飛ばして後で戻る勇気を持つこと。

5.見直しは計算式ではなく“結果”を確認

　符号、単位、数値の範囲など、数秒のチェックで救える失点が多い。必ず最後に3～5分確保する。

シミュレーション例：70分の時間の流れ

• 0〜11分：第1問（三角関数）
• 11〜21分：第2問（指数・対数）
• 21〜35分：第3問（微分・積分）
• 35〜45分：選択1問目（数列 or ベクトルなど得意分野）
• 45〜55分：選択2問目
• 55〜67分：選択3問目
• 67〜70分：最終チェック（符号・単位・範囲を見直す）

👉 数学ⅡBCは「正解力」以上に「時間運用力」が勝敗を分ける試験。
普段から模試や演習でストップウォッチを使い、本番と同じ70分間の流れをシミュレーションする練習が、最大の対策になります。
何度もシミュレーションを行い、自分だけの”得点を最大化する”時間配分を見つけましょう。

---

時間が足りない人へ｜実戦で使える時短テクニック

数学ⅡBCは70分で6題。1問あたりの持ち時間はわずか11〜12分です。
ここでは「スピードを上げる」というよりも、「迷いを減らし、無駄をなくす」ための実戦的テクニックを紹介します。

① 微分・積分はあえて完答しない

• 時短テクニック
  • 最大・最小問題では、導関数を求める→増減表を書く→極値候補を出すまでやれば得点は確実。
  • 最後に待っていることが多い面積問題は、計算に時間を要するケースが多い。積分区間だけを設定して式を書くだけでも加点がある。
  • 見直しのタイミングで、時間があれば最後まで解ききるのがコツ。

• よくあるミス
  • 完答を目指して時間を浪費 → 他の大問に手をつけられず失点。

② 全体像を見通し、製作者の意図をつかむ

• 時短テクニック
  • 問題文を最初にざっと読み、「この大問はどんな流れで進むのか」を把握する。
  • 共通テストは誘導型問題なので、ゴールを予測しておけば、不要な計算を省ける。
  • 例：「最初に平均を計算 → 仮説検定で正誤判定 → 最後に結論をまとめる流れだな」と理解して進む。

• よくあるミス
  • 目の前の小問だけに没頭 → 誘導を無視して無駄な計算をしてしまう。

③ 選択問題は“瞬間判断”で決める

• 時短テクニック
  • その場で得意なテーマかどうかを判断して選択問題を決定したい人向け。本番で問題を配られたら、まず30秒だけ全体をざっと見て、自分の得意分野を即決。
  • 例：
    • 「数列は漸化式、和の問題なら得点できる」
    • 「統計は仮説検定が出たら避ける」
    • 「複素数平面は図形問題なら挑む」
  • ただし、あくまで最短なのは自分が解く3題を普段の模試で決めておき、本番では迷わないこと。

• よくあるミス
  • 選択問題で悩み続け、解き始めが遅れて時間不足。

④ 公式・定理は“条件反射”で使う

• 時短テクニック
  • 頻出典型問題の解法は「出た瞬間に適用できる」状態にしておく。
  • 問題文を見たときに「これはこの公式」と反射的に判断できれば、思考時間が一気に短縮。
  • 例：
    • 三角関数の最大最小 → 倍角公式を用いて変形して2次関数へ持ち込む
    • 群数列 → 和の公式から「n群の初項が、初めから数えて何番目か」を求める
    • 放物線と直線で囲まれた図形の面積 → 6分の1公式で楽に計算する

• よくあるミス
  • どの公式を使うべきかで悩み、遠回りな別解に挑戦 → 計算が膨大になって時間切れ。

⑤ 選択肢・解答群を“先に軽くチェック”

• 時短テクニック
  • 選択肢をざっと見るだけで「範囲外の数」「符号が逆」「単位がおかしい」などを発見できる。
  • これにより、計算の途中でゴールが見えるので安心して進められる。
  • 例：「答えは整数のはず」「0〜1の範囲に収まるはず」など。

• よくあるミス
  • 選択肢を見ずに計算 → 最後に答えがどれにも合わず、やり直しで大幅に時間を失う。

⑥ 見直しは“結果だけ”を確認

• 時短テクニック
  • 見直しで注目すべきは、符号・単位・範囲・選択肢との整合性の4点のみ。
  • 途中計算の細部は追わず、結果（答え）が「数学的にあり得るか？」だけ確認する。
  • 例：「確率が1を超えていないか」「面積が負になっていないか」

• よくあるミス
  • 途中の式を全部見返して時間を浪費し、本当に直すべき単純な符号ミスを見逃す。

👉 数学ⅡBCは、とにかく時間との闘い。
この6つのテクニックを演習段階から習慣にすれば、70分をフルに活かし、得点源に変えられます。

---

2026年度の出題予測と難化ポイント

第1問：三角関数

【予想される方向性】

・加法定理や倍角公式、三角関数のグラフを用いた問題が中心。

・2026年度は「グラフと方程式の性質を組み合わせた出題」が増える可能性あり。

【難化ポイント】

・「解の個数」の問題など、グラフと式を行き来しながら考える力が必要。

・与えられた条件を正しく図示できないと誘導に乗り切れない。

【日ごろの勉強法】

・加法定理や三角方程式の解法を暗記ではなく「導出」できるように練習する。

・グラフを自分の手で描き、変化のイメージを体で覚える。

・典型問題を解くとき、必ず「この式がグラフでどう表れるか」を確認する習慣をつける。

第2問：指数・対数関数

【予想される方向性】

・指数・対数方程式の処理に加えて、グラフを絡めた大小関係や領域問題が出題される見込み。

・解答群から正しいものを選ぶ形式で「範囲・符号・単位」に注目させる問題が増える。

【難化ポイント】

・グラフと計算の両立が求められ、途中の読み取りを間違えると一気に崩れる。

・計算を最後までやらなくても、範囲の判定で正誤をつけられる問題も出るため、冷静な判断力がカギ。

【日ごろの勉強法】

・対数の定義や性質を式変形で自在に扱えるようにする。

・問題を解く際、グラフを描きながら数値の大小関係を確認する練習を重ねる。

・選択肢問題では「なぜ他が違うのか」を説明する習慣を持つと判断力が磨かれる。

第3問：微分・積分

【予想される方向性】

・最大・最小問題、増減表の作成、曲線の面積計算が継続。

・2026年度は「関数の位置関係」など、考察系の問題が増える可能性大。

【難化ポイント】

・計算量が多く、最後まで完答するのは難しい。

・途中で増減表を間違えると連鎖的に失点する危険がある。

【日ごろの勉強法】

・典型問題（極値・面積・接線）は毎日短時間でも解いて計算スピードを維持する。

・導関数を出すときに「因数分解→増減表→グラフ」をワンセットにする習慣をつける。

第4問：数列（選択）

【予想される方向性】

・等差・等比の和に加え、漸化式や数学的帰納法の出題。

・漸化式から一般項を導かせるタイプや、Σ計算を応用するタイプが強化される。

【難化ポイント】

・誘導に従って漸化式を立てないと一般項にたどり着けない。

・Σ記号を安易に展開すると計算が複雑化しやすい。

【日ごろの勉強法】

・等差・等比・漸化式は「典型パターン別」に整理して覚える。

・一般項を直接出すのではなく「漸化式から立式する流れ」に慣れておく。

・数学的帰納法は、「仮定→次の段階」の手順をスラスラ書けるよう反復練習する。

第5問：ベクトル（選択）

【予想される方向性】

・平面ベクトルの内積・距離計算に加えて、面積や垂直条件を利用する問題。

・立体的な配置を扱う場合もあり、図形感覚とベクトル計算を結びつけられるかが問われる。

【難化ポイント】

・図を描かずに進めると、条件を見落として計算ミスが多発。

・式に頼りすぎると、意味を理解しないまま無駄な計算を繰り返す。

【日ごろの勉強法】

・問題を解くときは必ず図を描き、ベクトルの関係を整理する習慣をつける。

・空間ベクトルでも、平面（三角形）を抜き出すことを意識する。

・過去問演習では「ベクトル方程式」と「数学ⅠA：図形の性質」をリンクさせて学ぶ。

第6問：統計的推測（選択）

【予想される方向性】

・仮説検定、分散比較、区間推定など新課程分野が引き続き中心。

・「文章で説明された統計用語を数学的に解釈する力」が重視される。

【難化ポイント】

・条件文の意味を正しく読み取らないと、計算の前段階でつまずく。

・箱ひげ図や散布図に頼れない形式もあり、読解＋数理の融合が必要。

【日ごろの勉強法】

・教科書の例題やチャートを使い、仮説検定の解法を確実に身につける。

・「母平均」「標本平均」の違いを言葉で説明できるように整理しておく。

・グラフや表を読み取る練習を、時間を測りながら行うと実戦力が高まる。

第7問：複素数平面（選択）

【予想される方向性】

・複素数の極形式表示、回転の表現、ベクトル的な考え方との融合。

・図形問題と結びつけて出題される傾向が強い。

・二次曲線（楕円・双曲線など）が出題される可能性あり。

【難化ポイント】

・複素数を「ただの数」として扱うと混乱する。

・図形的意味（回転・距離・内積）を理解していないと解けない問題が増える。

・二次曲線に関する証明問題が出題される可能性がある。

【日ごろの勉強法】

・複素数を図にプロットし、回転や移動をベクトル的に理解する。

・「z＝a＋bi」の代入計算にとどまらず、極形式やド・モアブルの定理を活用する練習を重ねる。

・過去問や模試の複素数問題は「図形的にどう解釈できるか？」を必ず確認する。

・問題集で、二次曲線に関する証明問題を一通り演習し、流れを理解しておく。

👉 総じて2026年度の数学ⅡBCは、計算力に加えて「意味を理解する力」や「読解力」がさらに重要になると考えられます。
単なるパターン演習ではなく、「なぜそうなるのか」を自分の言葉で説明できる学習が差をつけます。

---

どこで差がつく？高得点者が意識するポイント

共通テスト数学ⅡBCは、計算力だけではなく問題構造をどう読み解くかで差がつきます。
ここでは、平均点層と高得点層の違いを整理しました。

平均点層 vs 高得点層の違い

観点	平均点層	高得点層
問題構造の先読み力	・誘導をそのまま追うだけ ・全体像を意識せずに小問ごとに処理 ・無駄な計算で時間を浪費	・「この誘導の先で何を問いたいか」を推測 ・ゴールを見据えて効率的に計算 ・条件の意味を理解して解答の方向性を早めに定める
選択肢の処理	・絞り込まずに選ぶ ・全選択肢を計算して時間を浪費	・単位・符号・範囲などで瞬時に不適切を排除 ・ゴールを意識して計算を最短ルート化
図やグラフの活用	・頭の中で処理して混乱 ・条件を読み飛ばして計算ミス	・必ず図やグラフを描き、条件を可視化 ・図示によって解法が直感的に見えてくる
心理面のコントロール	・難問に焦って冷静さを失い、連鎖的に失点	・「ここまでで必要点は取れた」と割り切り、気持ちを切り替えて次へ進む
見直しの姿勢	・途中計算を延々と確認して時間切れ ・問いに答えているかを見落とす	・符号・範囲・単位・整合性のみを短時間でチェック ・数秒の確認でケアレスミスを防ぐ

👉 高得点者の強みは、「先を読む力」＋「迷わない選択」＋「冷静な心理」。
これらを日ごろの演習から意識することで、本番70分の使い方が劇的に変わり、高得点が狙えるようになります。

---

まとめ｜形式が固まる今、“読解力 × 条件整理 × 時間配分”を鍛えるラストチャンス

2025年度から始まった数学ⅡBCは、2026年度で2年目。
形式が定着する一方で、問題文を正確に読み取り、条件を整理して、限られた時間で解き切る力がより強く求められます。

・必答問題（数学Ⅱ）で基礎得点を固める

・選択問題（数学B・C）は得意分野を伸ばし、苦手は時間をかけすぎずに部分点狙い

・70分を見据えた時間配分をシミュレーションし、自分だけの時間配分を習得する

この3つを徹底すれば、難化傾向の中でも安定して合格ラインを突破できます。

👉 数学ⅡBCは「暗記勝負」ではなく、「理解を整理し、限られた時間で表現する試験」。
読解力・条件整理力・時間配分力を意識して鍛えれば、得点は必ず伸びます。

今こそ、自分の戦略を固める最後のチャンスです。