こんにちは！進学個別指導塾ノエクリ鶴来校・有松校の窪田です。

昨日の石川県総合模試の大問3で、二次関数の問題が出題されましたね。みなさん、手応えはどうでしたか？

先日のブログで紹介した「二次関数の裏技」を使えば、(3)も時間をかけずに解けたはずです。

前回もお伝えしましたが、模試で焦ってしまう最大の原因は 時間が足りなくなることです。

問題の解き方は一つではありません。実際、やろうと思えばさまざまな解法が存在します。
そのため、自分で勉強していると「自分流でゆっくり解いて正解して満足する」というパターンに陥りやすいです。

しかし、入試のように 時間制限がある本番では「いかに素早く、確実に得点するか」が勝負になります。

ノエクリの個別授業では、まさにその本番で使うべき「速くて正確な解き方」を徹底的に解説します。

もちろん、時間に余裕がある時期であれば、いろいろな方法を試すのも良いと思います。しかし、中3生は入試まであと数ヶ月。今から第一志望校に逆転合格するには、どれだけタイパよく勉強できるかが合否を分けると言っても過言ではありません。

今日は、二次関数で使える裏技と、昨日の模試の類似問題の解き方を解説していきます。

変化の割合は、一瞬で解ける！

 

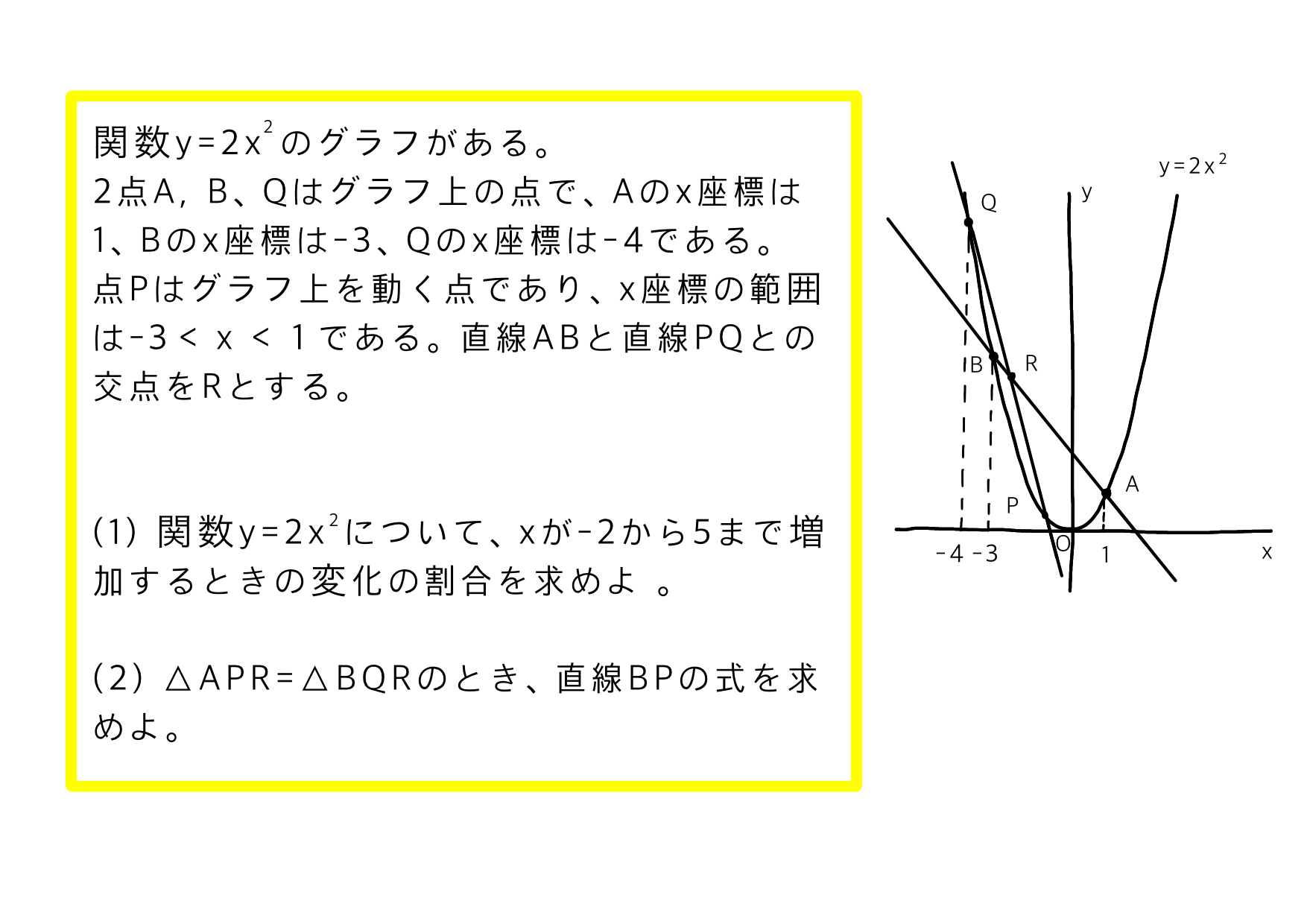
一次関数の変化の割合は傾きと同じなので、傾きがわかっていれば一瞬で解けましたが、二次関数の場合は、面倒な計算をしている人も多いと思います。

しかし、この裏技を使えば一瞬で解けます。

 

 

実際に解いてみると・・・、

 

 

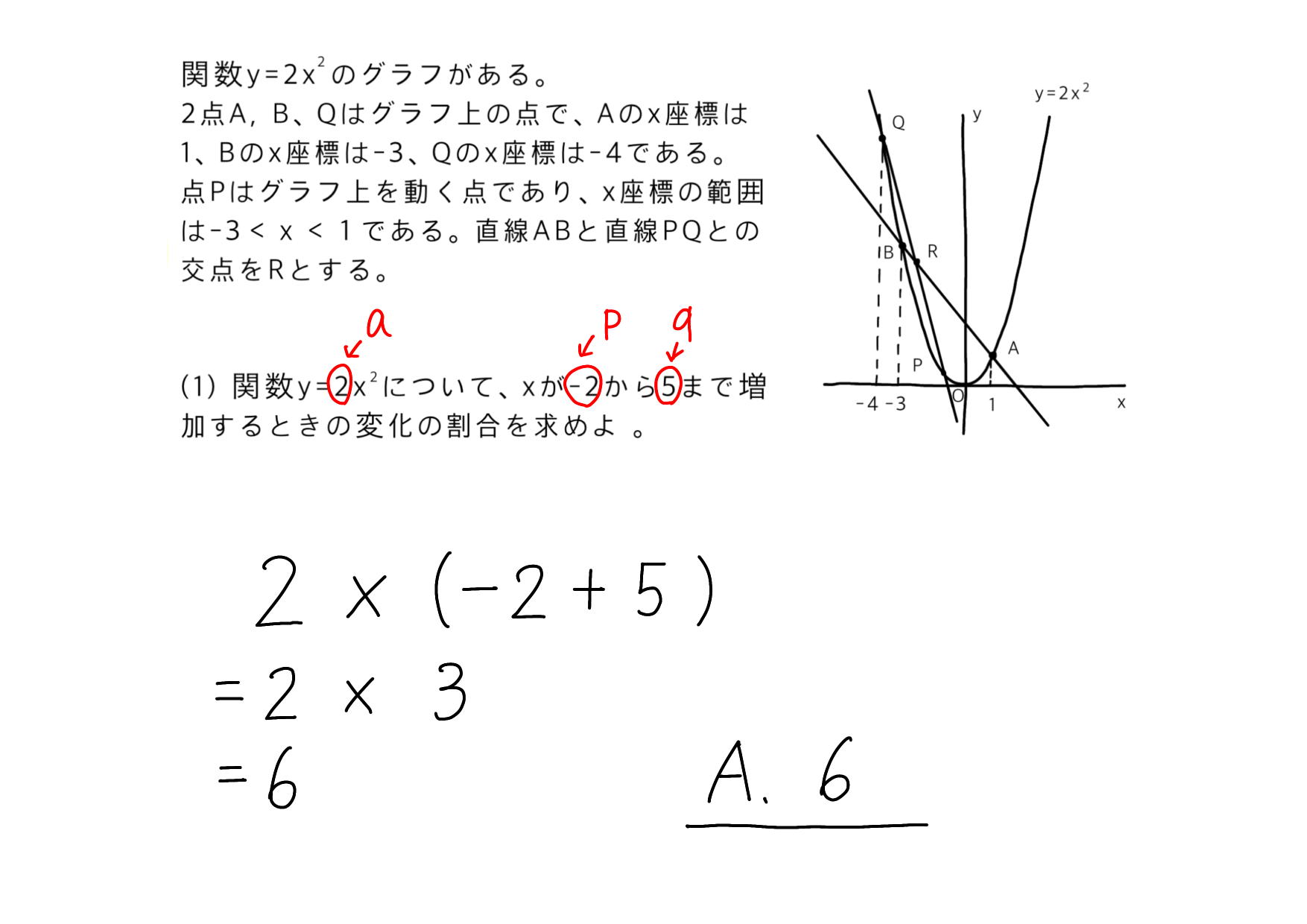
本当に一瞬で解けます！

ぜひこの裏技を練習して使えるようになってください。

 

次は、面積の問題です。類似問題が昨日の総合模試で出題されていました。

入試でも出題されそうな問題なので、ぜひ簡単に解ける方法をマスターしておきましょう。

 

 

「面積が等しい」問題は、まずは等積変形で考えてみる！

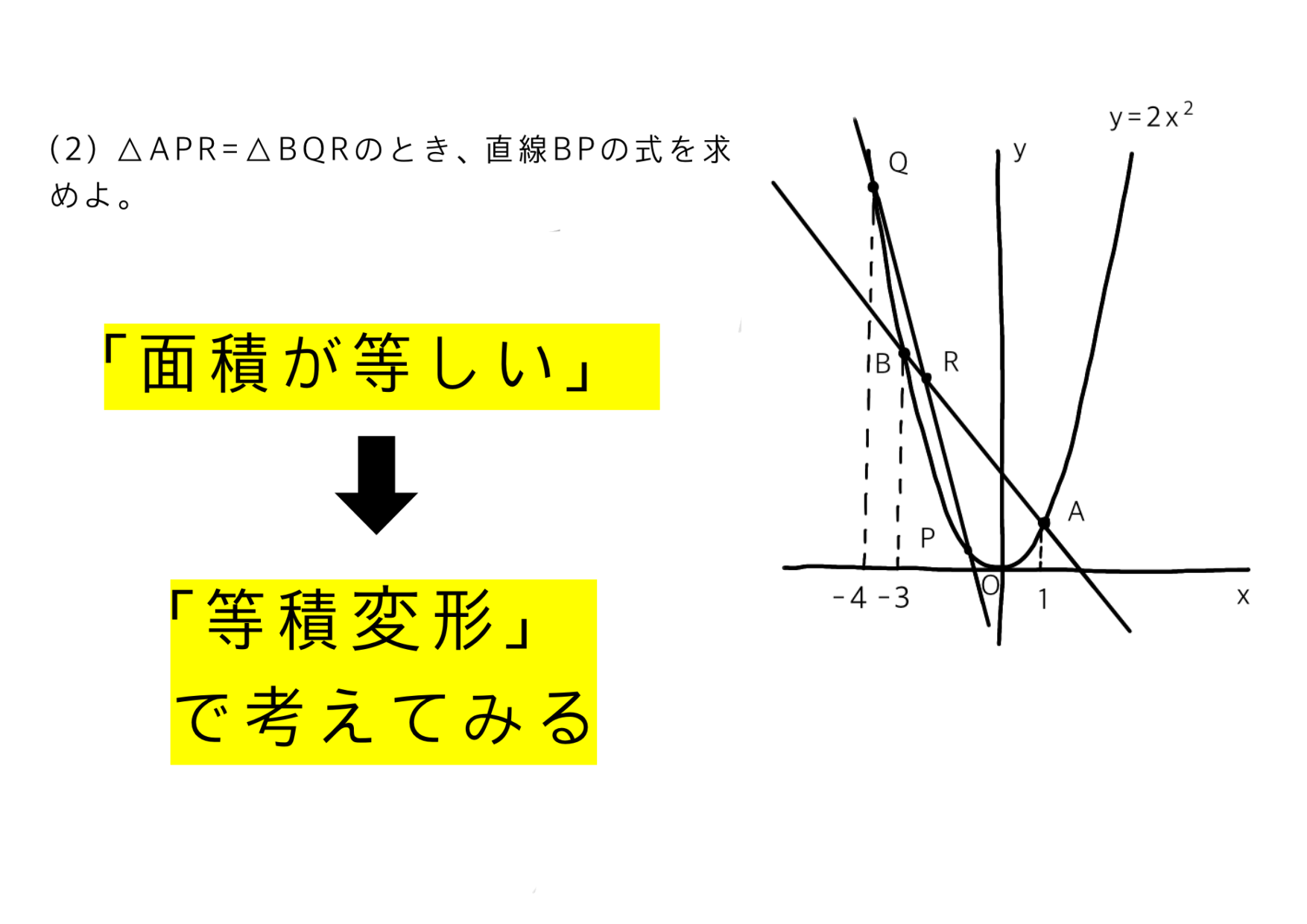
しかし、今回同じ面積なのは、△APRと△BQRです。

この場合は等積変形を使うことはできなさそうです。

そこで、他の三角形で考えてみます。

等積変形を考えるとき、底辺が同じ三角形見つけることが大切です。

 

 

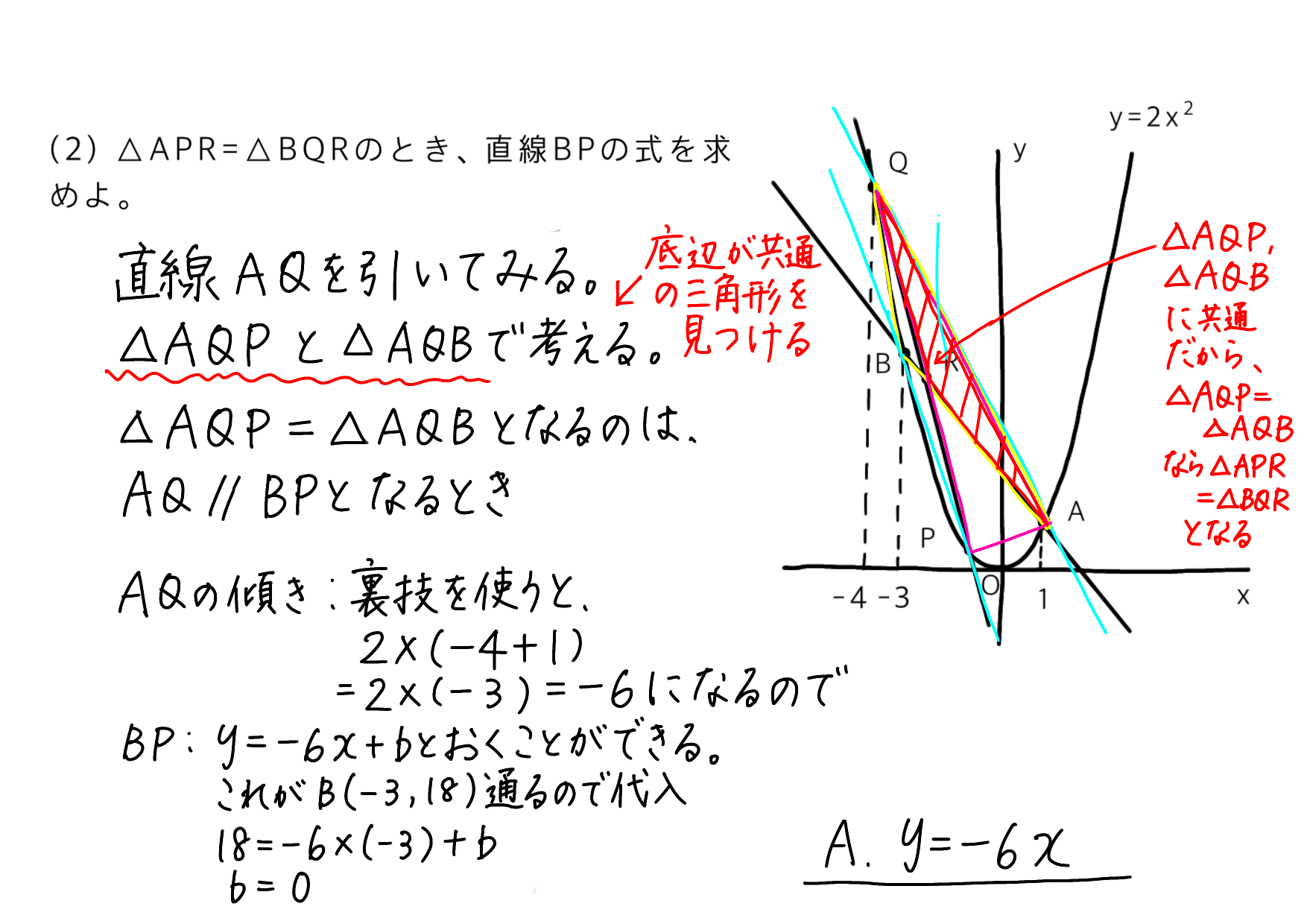
実際に面積を求める方法など、他にも解き方はいろいろあります。しかし、この等積変形で考えるのが、一番素早く解けるのではないかと思います。

今回できなかった人は、この問題は入試で出題されるかもしれません。もし出題されたときに正解できるようにしっかり復習しておいてください。

 

 

積み重ねた努力が本番で花開く！

ワールドシリーズ「ブルージェイズ vs ドジャース」第7戦の9回、ピンチを救ったセンター・パヘス選手のあのジャンピングキャッチも、日々積み重ねてきた努力の賜物です！

大事な本番の場面で最大限の力を発揮するためには、日々の努力なしでは成立しません。

模試を受けても、なかなか成績が上がらず不安になる人もいると思います。しかし、諦める必要はありません。本番で結果を出すためにも、今できることをひたすら積み上げていきましょう。

入試まで残り数ヶ月となりました。

ノエクリでは、まだ受講生を募集しています。「今から塾に入っても間に合うのかな…」と迷っているあなた、ノエクリはいつでも大歓迎です。

志望校合格に向けて、今必要なのは どれだけタイパよく勉強できるかです。

ぜひ、私たちと一緒に志望校合格を掴み取りましょう。