こんにちは、進学個別指導塾ノエクリ鶴来校の窪田です！中学3年生のみなさんの中で、今週第７回石川県総合模試を受ける人もいると思います。今日は、「いつもは平面図形の（３）ははじめから解けないと思って捨てていたけど今回は得点してみたい」と思っている人へ向けて、ちょっとしたアドバイスを書きたいと思います！

第７回総合模試（数学）の平面図形ではどんな問題が出ているのか

過去4年分の総合模試を見てみると、平面図形では4年連続で円の問題が出ていました。

なので、今回も円が出る可能性が大です！

2020年

（１）角度を求める問題　→半円の弧に対する円周角＝90°、円周角の大きさ＝弧の長さに比例、を利用する。

（２）相似な図形の証明　→円周角を使って考える。

（３）辺の長さを求める問題　→（２）で証明した相似な三角形、（２）で示されていた条件を使って考える。

円周角、二等辺三角形から、相似な図形を見つけて、最後は比例式にして辺の長さを求める。

2021年

（１）角度を求める問題　→円周角を使って考える。

（２）合同な図形の証明　→半円の弧に対する円周角90°を使って考える。

（３）辺の長さを求める問題　→（２）で証明した合同な三角形、（２）で示されていた条件を使って考える。

「辺の長さが同じ」から「中点連結定理」を利用する。

円周角から相似な図形を見つけて、最後は比例式にして辺の長さを求める。

2022年

（１）角度を求める問題　→円周角、外角を使って考える。

（２）相似な図形の証明　→円周角、錯角を使って考える。

（３）辺の長さを求める問題　→（２）で証明した相似な三角形、（２）で示されていた条件を使って考える。

新たに作った点Gを利用

円周角、平行から相似な図形を見つけて、最後は比例式にして辺の長さを求める。

2023年

（１）角度を求める問題　→円周角、二等辺三角形の底角を使って考える。

（２）相似な図形の証明　→円周角、同位角を使って考える。

（３）辺の長さを求める問題　→（２）で証明した相似な三角形、（２）で示されていた条件を使って考える。

円周角から相似な図形を見つけて、相似な図形の面積比は相似比の２乗に等しい、を利用して求め

る。

円の問題が出たときのポイント

（１）の問題

過去4年分の問題を見てみると、どれも角度を求める問題でした。

円の問題が出たときは、必ずと言っていいほど円周角を使うので、まずは円周角を見つけましょう！

（２）の問題

相似な図形か合同な図形の証明です。

特に円で相似の証明が出た場合、「２組の角がそれぞれ等しい」が大半なので、円周角など、２組の等しい角を見つけましょう！

（３）の問題

辺の長さを求める問題か、面積を求める問題が出ていました。

どの問題も（２）で求めた相似な図形や合同な図形を使っているので、（２）で書かれていた条件（AB//DCなど）と相似な図形、合同な図形を使って考えましょう！

（３）でも、「円周角の定理」は、ほぼほぼ使います！

そこから相似な図形を見つけましょう。

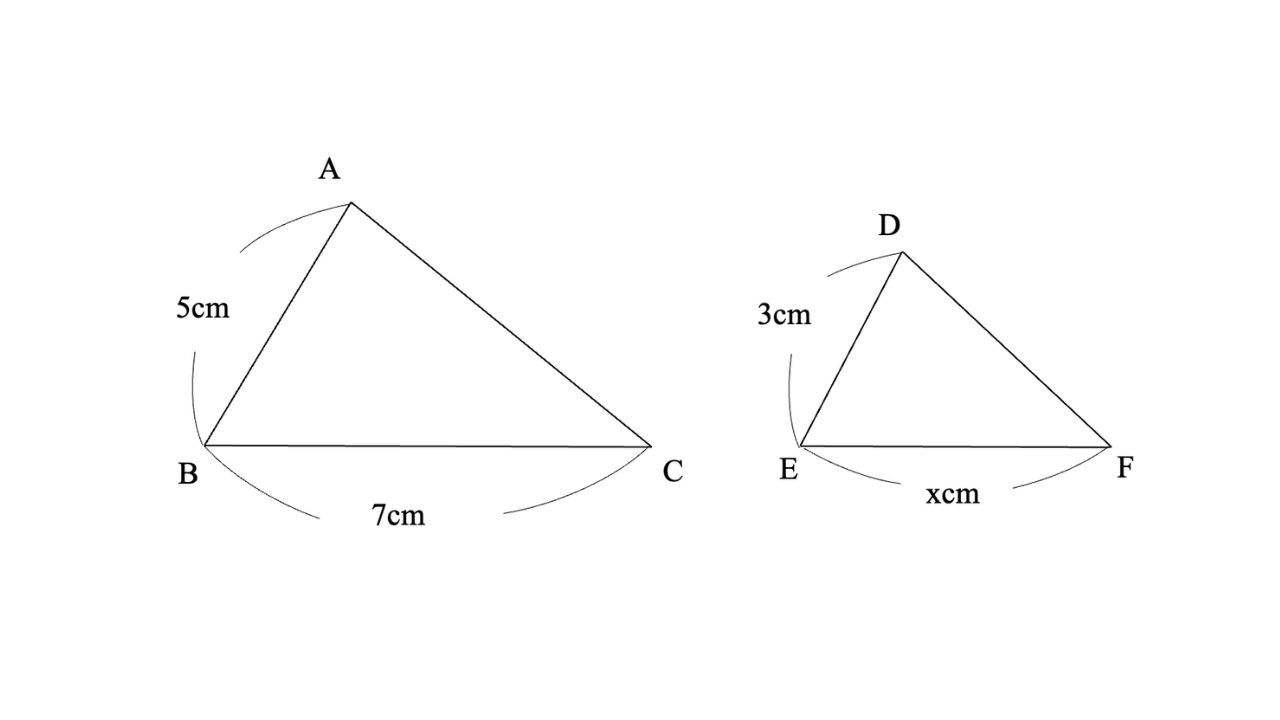
特に（３）の問題を考えるとき、相似な図形や合同な図形を下の図のように書き出すのがおすすめです。

こうすれば、相似比が何：何かすぐにわかり、辺の長さも考えやすくなります。

また、辺の長さが等しいとき、「中点」と書いてあるときは、真っ先に「中点連結定理」が使えないか考えましょう！

他にも、面積比の問題が出たときは、高さの等しい三角形の組みを探しましょう！

このことを念頭に置いて問題に挑むと、結構解けます。ぜひいろいろな問題に挑戦してみてください！

まとめ

これまで平面図形を「捨て問」としていた人、ぜひ、今回の模試では（３）も挑戦してみてください。

（１）は3点、（２）は4点、（３）は7点もあります。答えが出なくても途中式で部分点がもらえることもあるので、ぜひ挑戦してください。

円が出たら、円周角はほぼ使います！

それでは、今回の模試も全力で頑張ってください！