【2次関数で時間が足りない中3生必見】学校では教えてくれない高校入試裏技①
2025.11.4 有松校 鶴来校
窪田

こんにちは!進学個別指導塾ノエクリ鶴来校・有松校の窪田です。
石川県の高校入試には、大問で関数の問題が出題されます。公立高校の場合は毎年(1)(2)(3)の3問で、配点は3点、4点、7点となっています。
(1)(2)は、直線の式を求めたり、変域を求めたりするなど、標準的な問題で得点しやすい問題となっています。しかし、テスト本番になると、焦ってしまいなかなか普段のように力を発揮することができない人も多いのではないでしょうか。
焦ってしまう大きな要因が、時間が足りないということだと思います。
石川県の高校入試は全国的に見ても難易度が高く、簡単に解ける問題ばかりではありません。しかし、トップレベルの高校を志望している人は、関数は全問正解したいところです。そして、少しでも素早く解くことができれば、平面図形や空間図形の問題にも時間をかけて取り組むことができます。
今日は、模試や入試で出題されやすい二次関数と一次関数の問題を一緒に考えたいと思います。
直線の式は、一瞬で解ける!
「直線の式を求めよ」「直線の式の傾きを求めよ」という問題は、よく試験に出るので、皆さんも解き方は知っていると思います。
①連立方程式で求める方法
②変化の割合を使って求める方法
このどちらかで解いている人が多いと思います。
しかし、この方法では、座標がわかっていないときは、まずは座標から求めなければならず、時間がかかってしまいます。
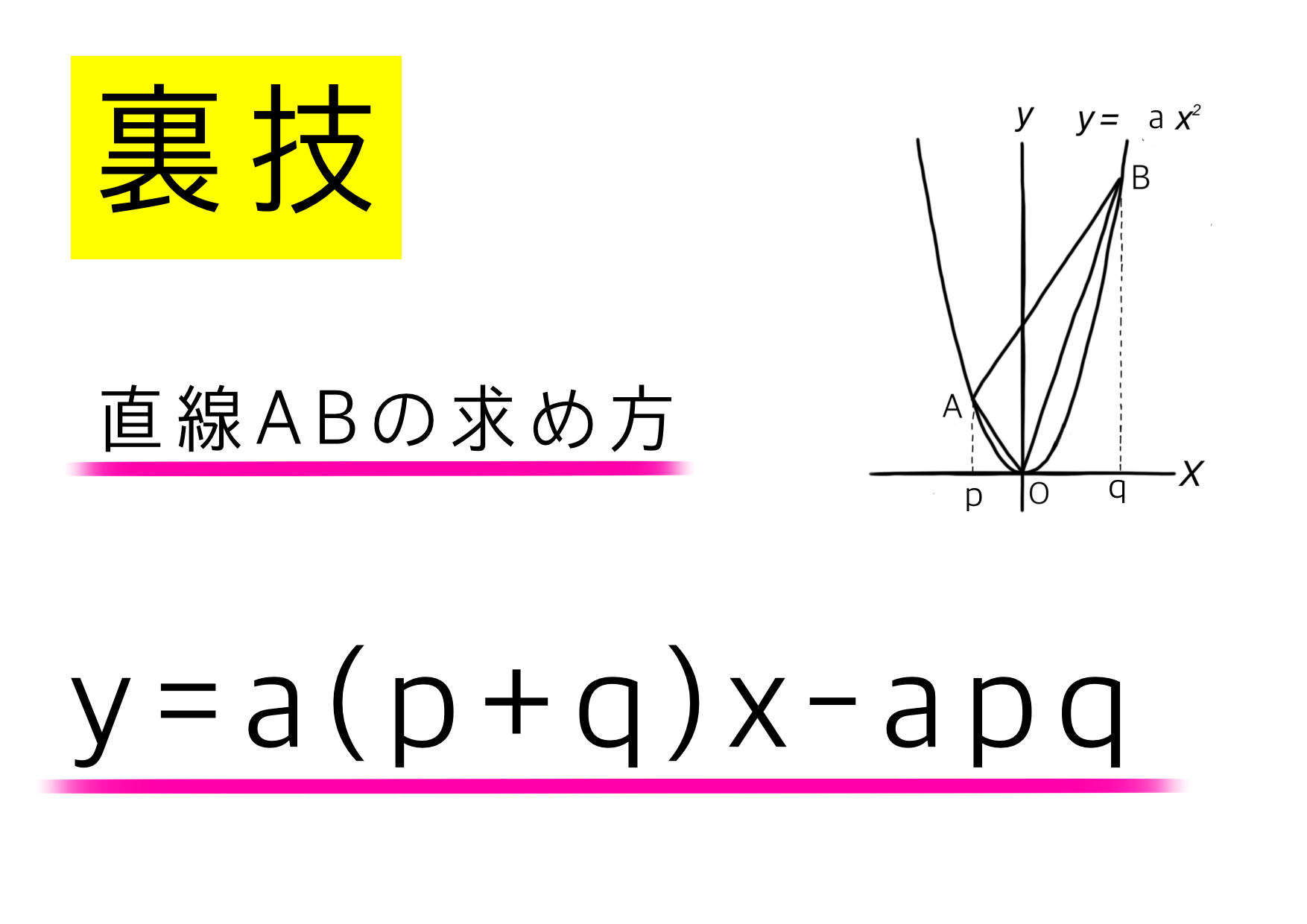
ここで時間を使いたくない人は、ぜひこの公式を使ってみてください!
・「傾きを求めよ」→ a(p +q)の部分だけ
・「切片を求めよ」→ -apq の部分だけ
この2点に注目するだけで、一瞬で直線の式が完成します。
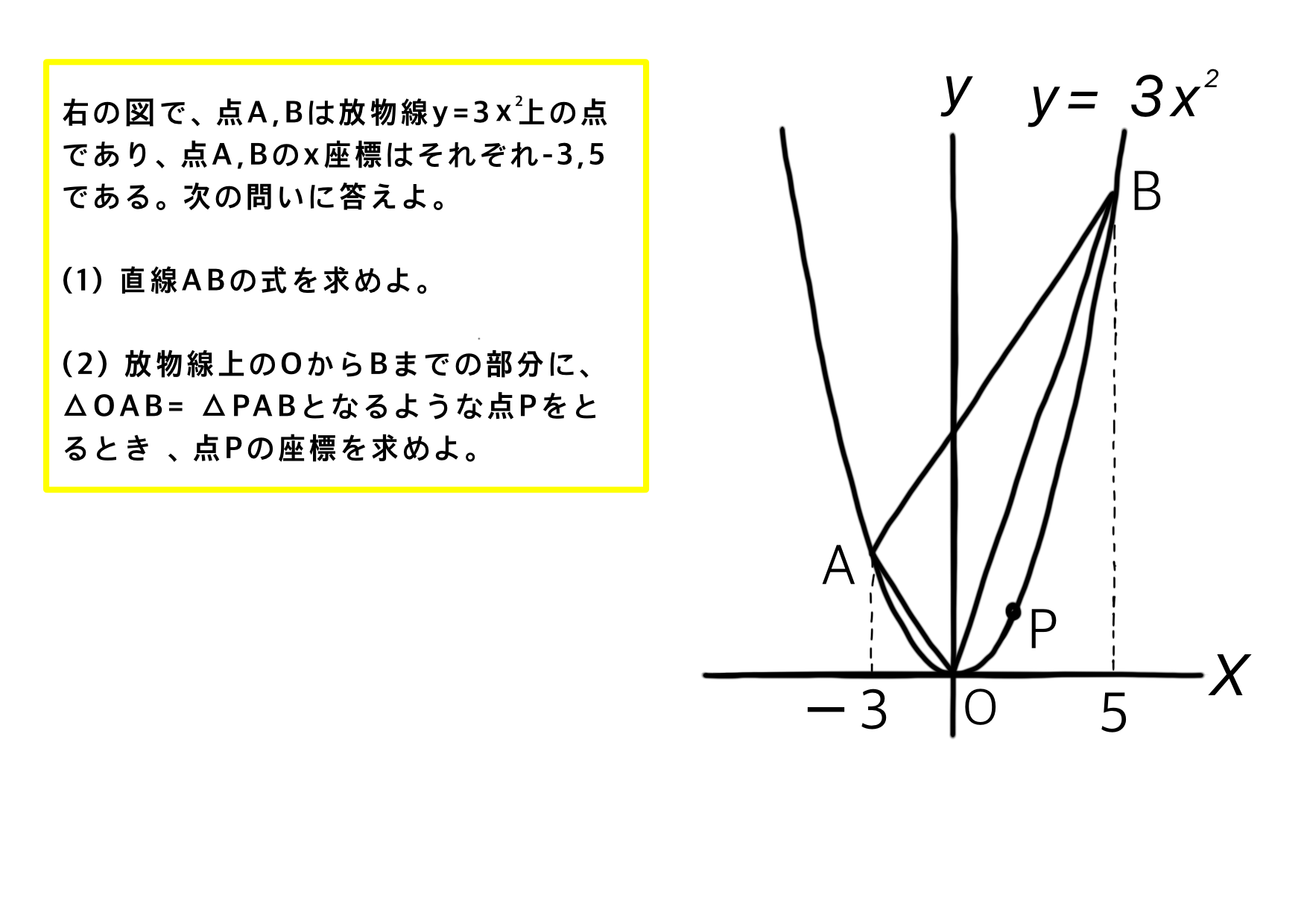
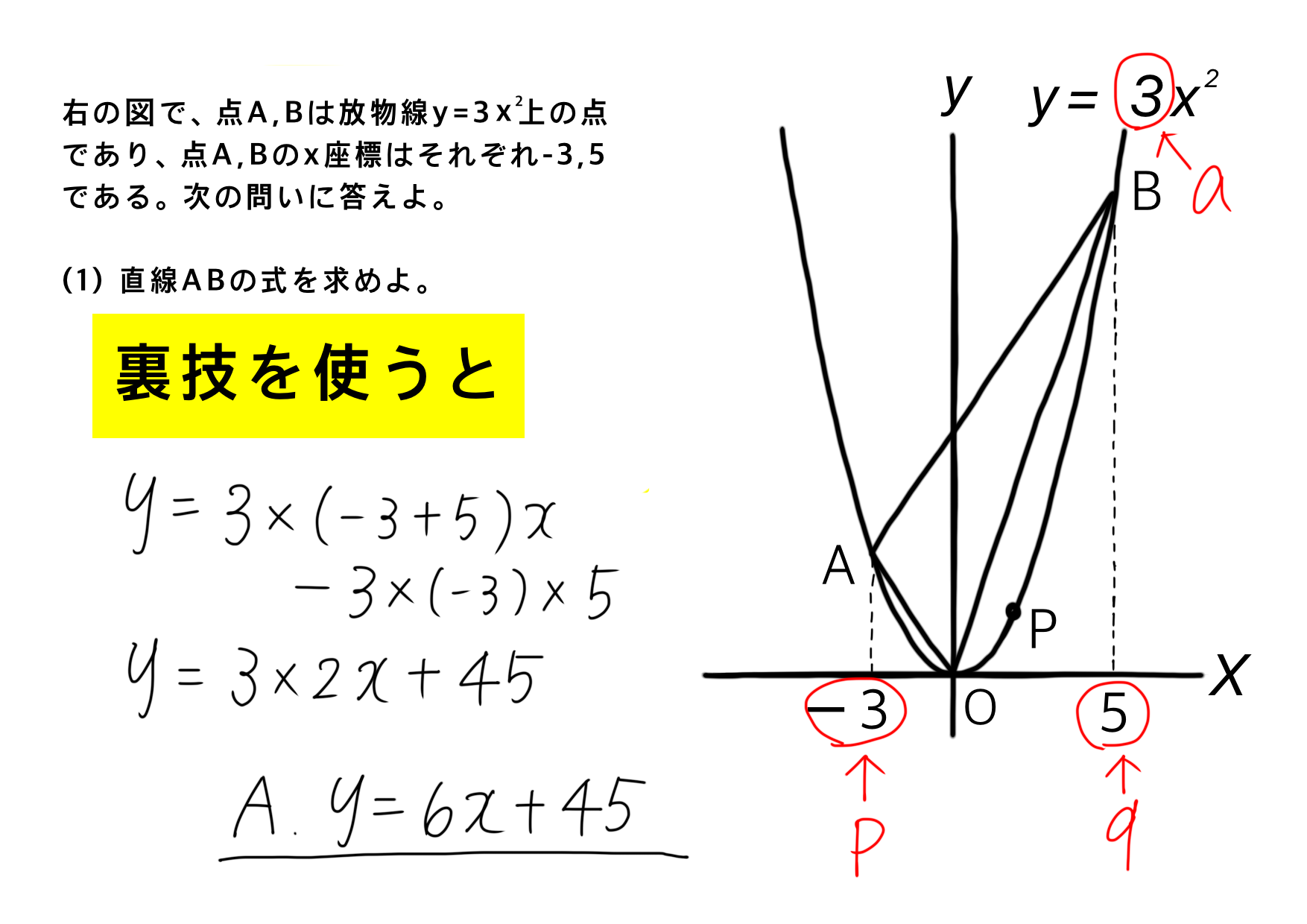
特に大きな数字や分数などになると、連立方程式で計算すると時間がかかってしまします。
しかし、この裏技を使えば、y座標を求める必要もなく、一瞬で解けるのでおすすめです!
そして、ここで時間を節約できれば、気持ちにも余裕が生まれます。
次も定番の問題で、面積の問題です。
まず等積変形を疑おう
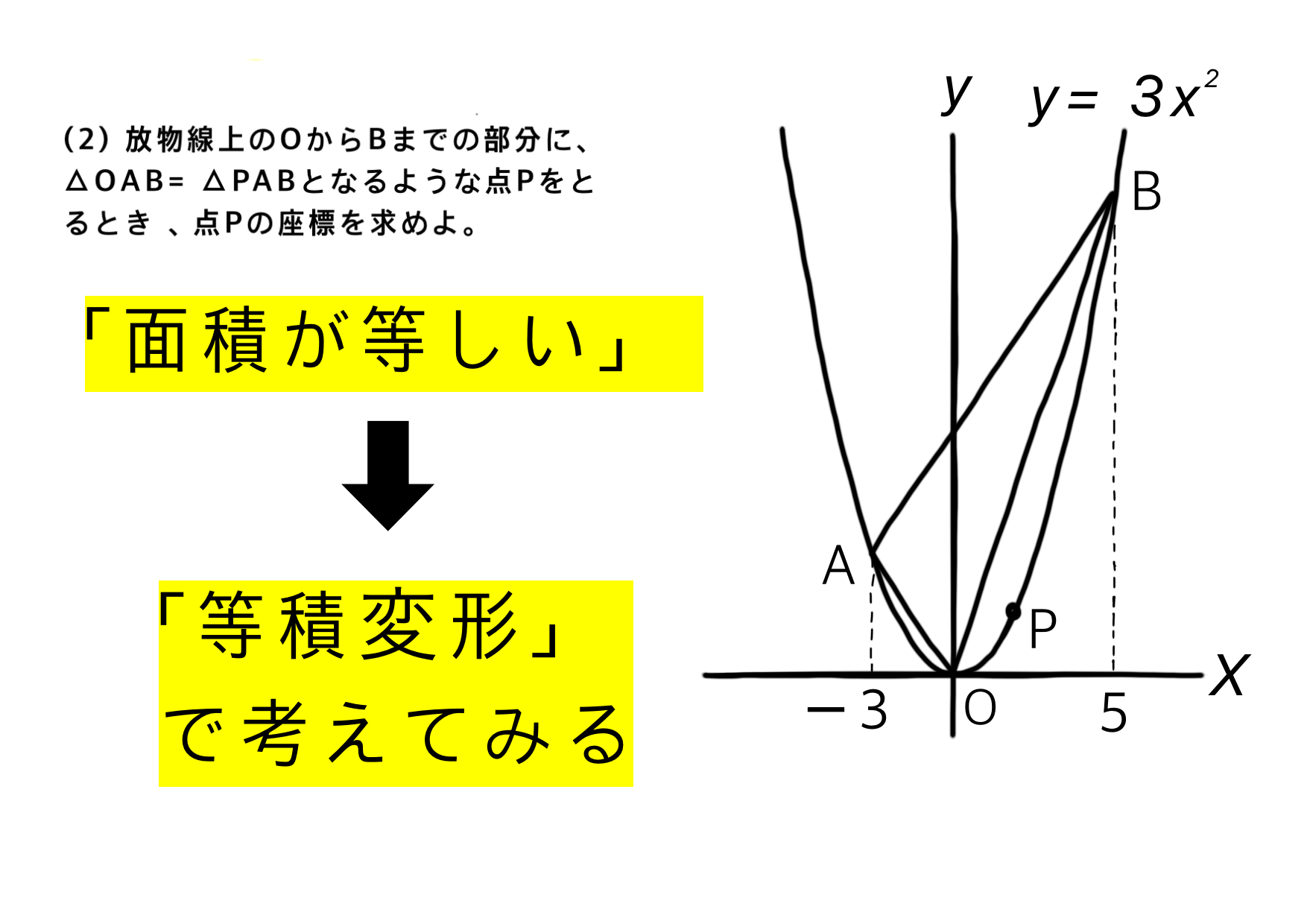
面積が等しい問題は、まずは「等積変形」が使えないか考えます。
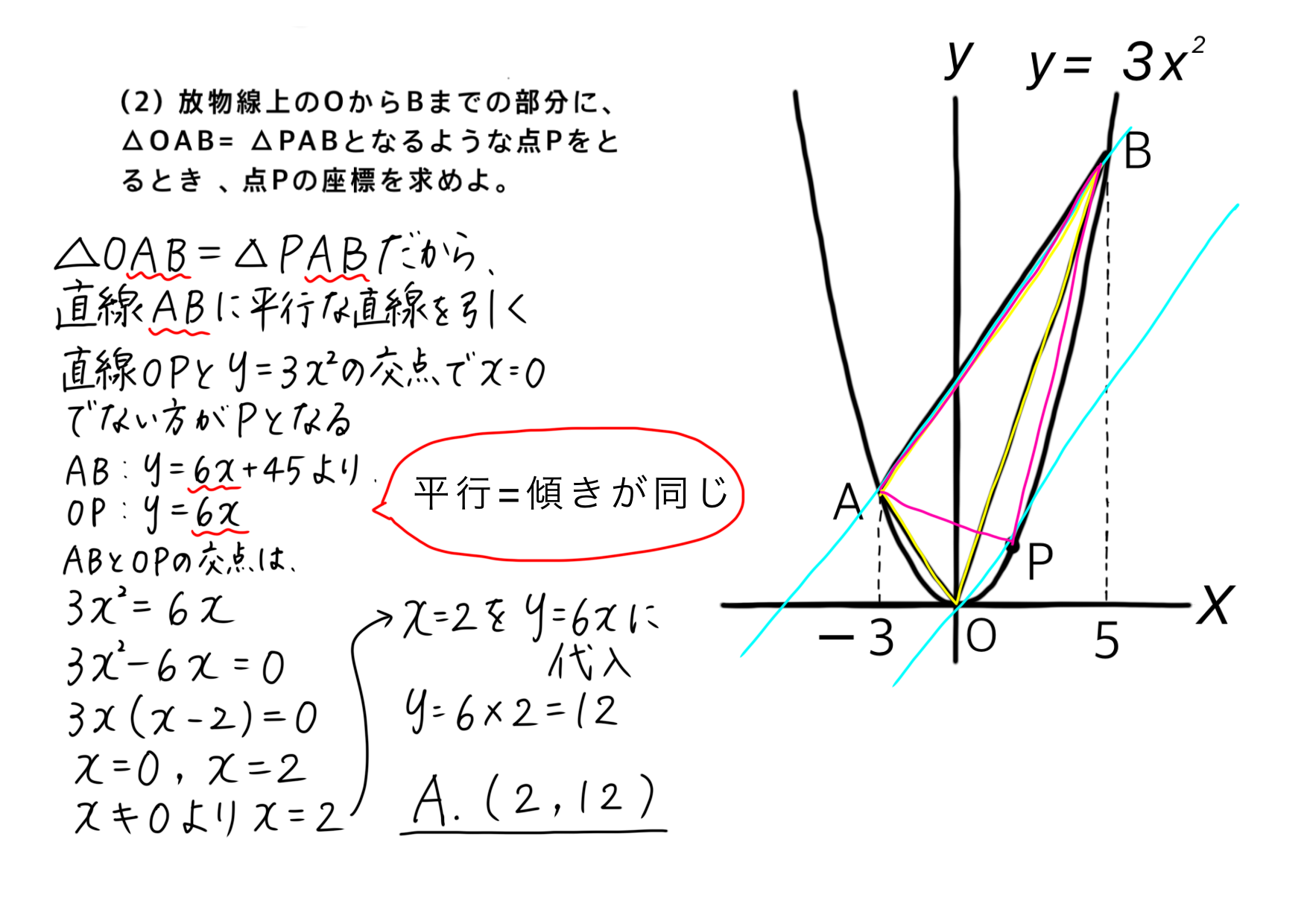
この問題は、実は等積変形を使わなくても求めることができます。
たとえば、Pのx座標を t とおいて、「x=t の縦線を引き、三角形の面積を実際に計算する」といった方法もあります。
しかし、この方法だと、
・A,Bのy座標を求める
・面積の式を立てる
・計算をまとめる
といった作業が多く、本番では確実に時間が足りなくなります。
この等積変形の方法なら、A・B の y座標を求める必要も、面積を実際に計算する必要もありません。
見た瞬間に式が立つので、圧倒的にタイパが良いです。
入試本番で「あと数分足りない…」を防ぐためにも、この等積変形のパターンはぜひ押さえておいてほしいです。
面積の問題は、高校入試で、関数の最後の問題で出題されやすく配点も高いので、トップレベルを目指す人や数学で得点を稼ぎたい人は、ぜひ解けるように頑張ってください!
一瞬の判断を支えるのは、日々の努力
先日、ノエクリに通う生徒が「授業中は理解できるけど、本番で閃くかわからない」「本番で解けなかったらどうしよう」などと話していました。
まだ11月です!まだ本番まで4ヶ月あります。大丈夫です!
「どんな問題が出ても解けそう」と自信をもって本番に臨めるように、類似問題をたくさん解いていきましょう。
不安に飲まれる必要はありません。

先日のワールドシリーズの第7戦の9回裏のピンチを救った、ミゲル・ロハス選手のホームへの送球は、これまでの努力の成果が詰まったものだったと思います。
守備位置が数センチ違えば、投げるタイミングが少しでも遅れていれば、結果は全く変わっていたでしょう。あの1球は、積み重ねた努力の結晶です。
受験も同じです。本番で自信をもてるように、今は積み重ねるだけです。
皆さんも、ぜひ本番に自信をもって臨み、力を発揮できるように、あと4ヶ月間悔いのないように頑張ってください!
進学個別指導塾ノエクリでは、学校では教えてくれない裏技など、受験に役立つ情報やテクニックを教えています。
「いまさら塾に行くのもな」と迷っている受験生の皆さん、ノエクリではまだまだ受講生を募集中です。
お気軽にお問い合わせください!
皆様のお問い合わせを心よりお待ちしています。

投稿者
窪田
有松校・鶴来校の窪田です!
▲▲クリックして窪田のブログ一覧(156ブログ公開中)を見る

